Code
→ Github page: github.com/seub
Overview
I studied theoretical Computer Science at ENS Cachan. Here is a quick overview of my past coding projects:
- I developed two cross-platform computer software with a nice GUI in C++/Qt in relation to my math research: Circle Packings and Harmony.
- I collaborated with mathematicians and data science researchers at the Heidelberg Institute of Theoretical Studies (HITS), which offers a "High Performance Cluster" (HPC).
- I mentored student projects at the Heidelberg Experimental Geometry Lab (HEGL), which involve math, coding, 3D printing, VR, and other technology.
- I worked on a few other coding projects, in relation to my math papers (e.g. The sum of Lagrange numbers), or Data Science projects (e.g. Cheese classifier), or "just for fun" (e.g. Chess engine).
Programming languages: I am proficient in C++ and Python. I have some experience with: Bash, C, HTML/CSS, Javascript, Julia, Latex, Mathematica, Maple, Matlab, Pascal, Qt, Sage, SQL.
Heidelberg Experimental Geometry Lab (HEGL)
At the Research Station "Geometry & Dynamics" (Heidelberg University), I was in charge of setting up the Heidelberg Experimental Geometry Lab (HEGL). The goal of HEGL is to promote the interaction between theoretical math research and computational experimentation and visualization.
In 2021/2022, I co-organized the two HEGL seminars and mentor undergraduate research projects.
![]()
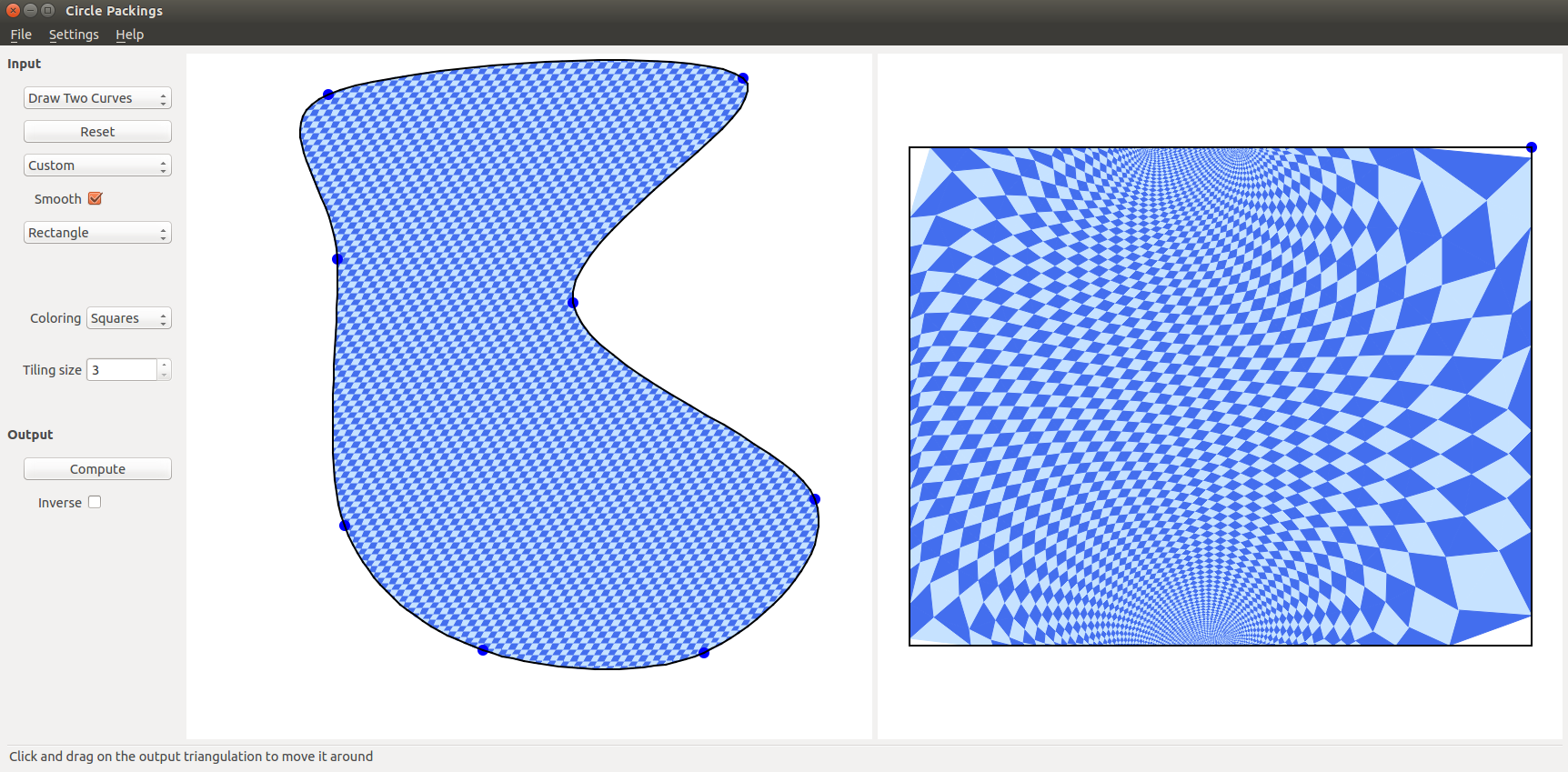
Circle Packings
This software created by Benjamin Beeker and myself computes and shows circle packings and Riemann conformal mappings. This project is hosted on GitHub here.
Below are a few screenshots (click to enlarge):
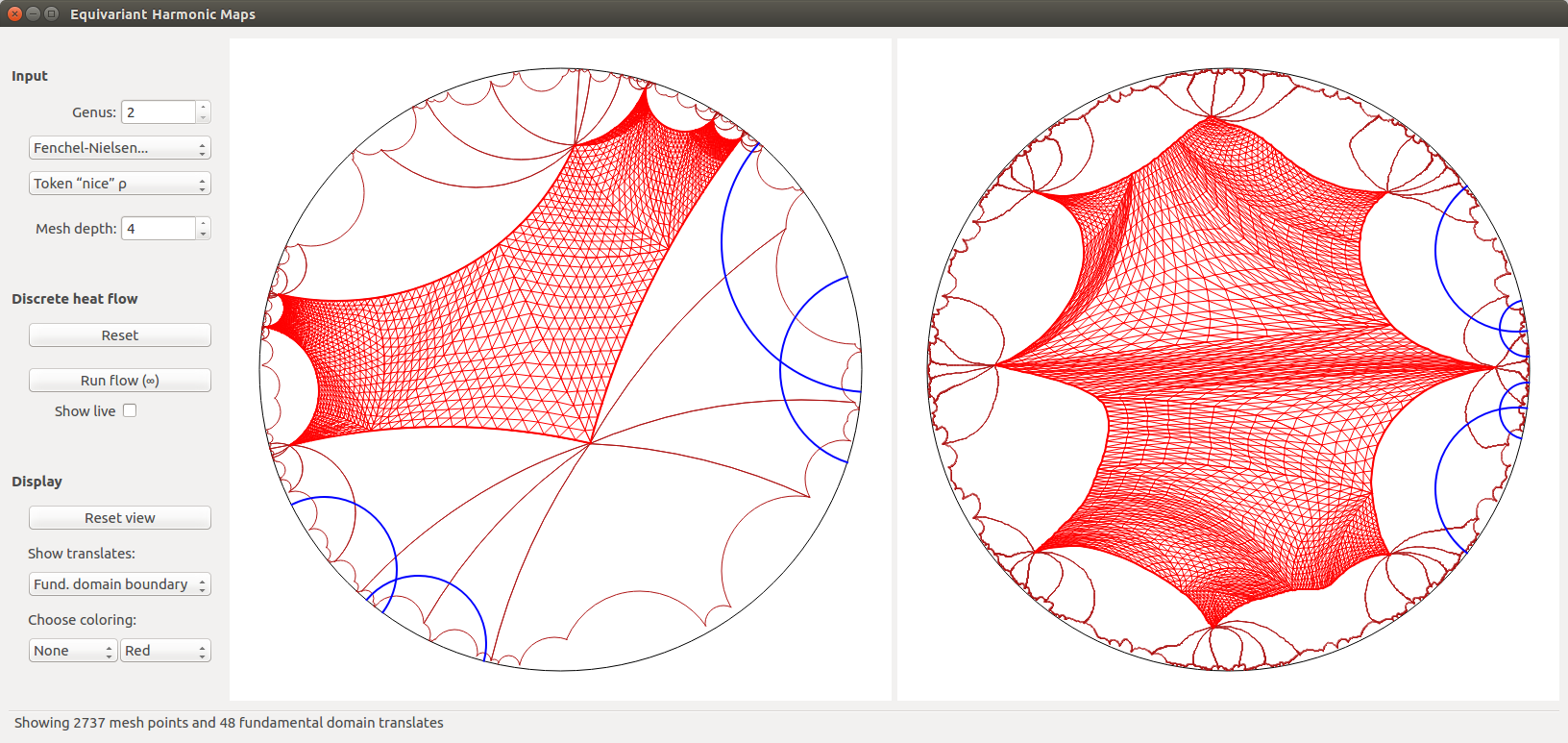
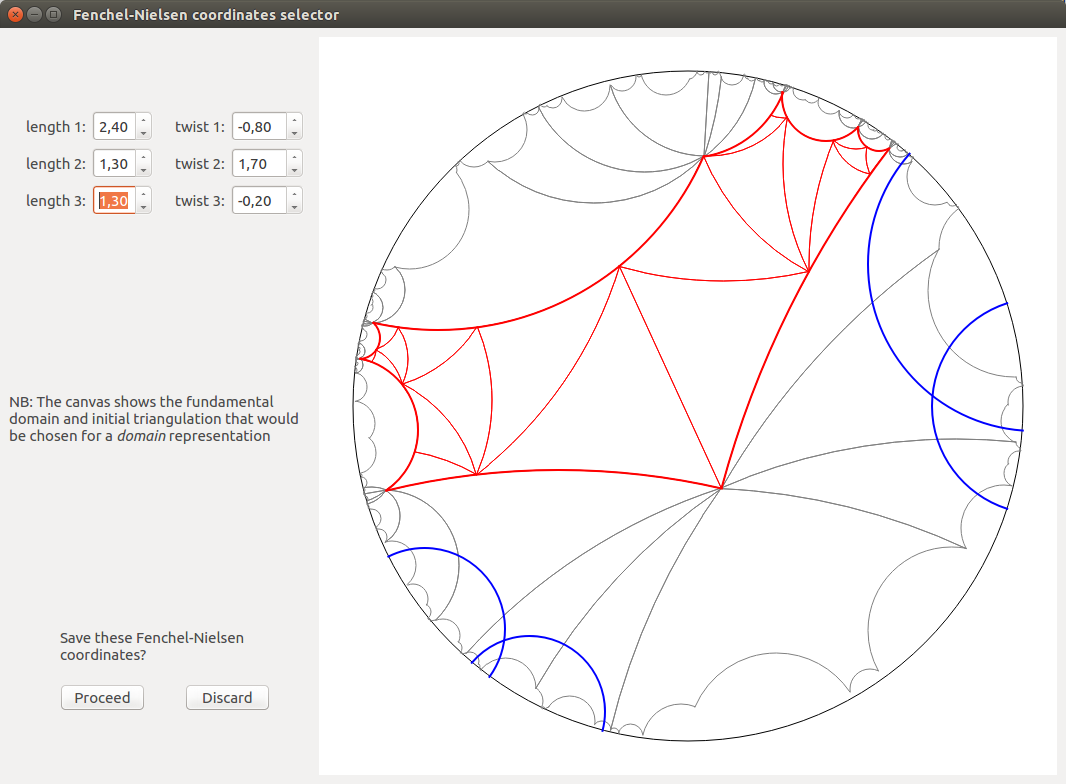
Harmony
This software created by Jonah Gaster and myself computes and shows equivariant harmonic maps from the hyperbolic plane \(\mathbb{H}^2\) to the hyperbolic plane \(\mathbb{H}^2\) (or in the future, hyperbolic 3-space \(\mathbb{H}^3\) and more general symmetric spaces). This project is hosted on GitHub here.
Below are a few screenshots (click to enlarge):