Harmony

Harmony is a mathematical software created by Jonah Gaster and Brice Loustau.

On this page you will find a brief overview of the program, install guidelines, and a quick guide for getting started.


Brief overview

The core algorithm of the program computes and shows equivariant harmonic maps from the hyperbolic plane \(\mathbb{H}^2\) to the hyperbolic plane \(\mathbb{H}^2\) (or in the future, hyperbolic 3-space \(\mathbb{H}^3\) and more general symmetric spaces). More precisely, given a closed surface group and a mesh depth, and given left and right Fuchsian representations, the program computes the unique discrete equivariant harmonic map from the left \(\mathbb{H}^2\) to the right \(\mathbb{H}^2\).

Two iterative methods are implemented: a discrete heat flow and a center of mass method. The discrete heat flow is essentially a gradient descent for the energy functional, while the center of mass method consists in replacing the function by its own average on neighbor values. The convergence of both algorithms relies on the convexity properties of the discrete energy.

The mathematical aspects are discussed in detail in the paper Computing discrete equivariant harmonic maps by Jonah Gaster, Brice Loustau and Léonard Monsaingeon. ArXiv link: arXiv:1810.11932.


Install

Harmony is free and open source (under the GNU General Public License). The software is currently in pre-release (beta) version. That means that it is functional and stable, but has not been deployed: unfortunately we have not made any "easy setup" file yet.

Until version 1.0 is released, in order to use Harmony you'll need to compile it from source. This first requires installing the Qt framework or development tools on your system. If your operating system is Windows or Mac OS, the process can be a bit difficult and we do not recommend it unless you're an experienced user. If you'd like to try, you should get Qt Open Source from the official site.

If you are using a GNU/Linux operating system, follow these simple steps to compile from source:

  1. Install the Qt framework. For Debian-based distributions such as Ubuntu and Mint:
    sudo apt-get install qt5-default qtdeclarative5-dev
    should do the trick. For other distributions, you can probably figure out how to install Qt development tools upon a quick web search.
  2. Download this archive and extract it. NB: It's better to clone the git repository for the latest version:
    git clone https://github.com/seub/Harmony.git
  3. Open a terminal, navigate to the directory with the source files and run:
    qmake -qt5
    and then
    make
    (this last step can be speeded up with make -j N instead, where N is your number of processor cores)
  4. You're done! A binary file "Harmony" was generated. To run it, double-click the file or run it from a terminal:
    ./Harmony.

Getting started

The main window of Harmony consists of a left panel (menu) and two canvases, both showing the hyperbolic plane in the Poincaré disk model:


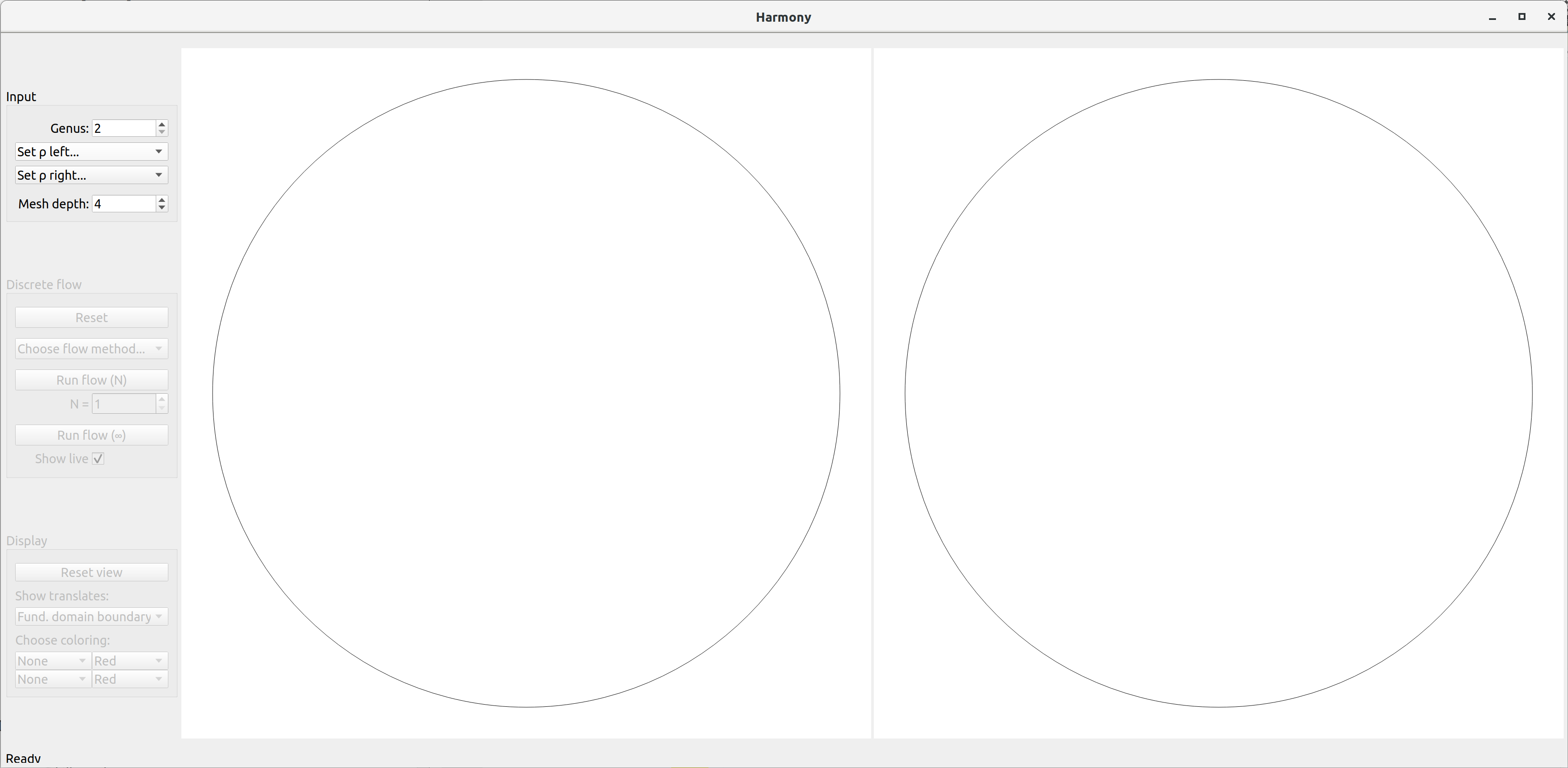
In order to start, you need to select Fuchsian representations for the closed surface group of genus \(g\), one for the left and one for the right canvases. You can also adjust the genus and the mesh depth, but for now you can leave the default values \(g = 2\) and \(\text{depth} = 4\). You can choose representations from the drop down menus "Set \(\rho\) left..." and "Set \(\rho\) right...". The main option is to open the "Fenchel Nielsen selector" window:


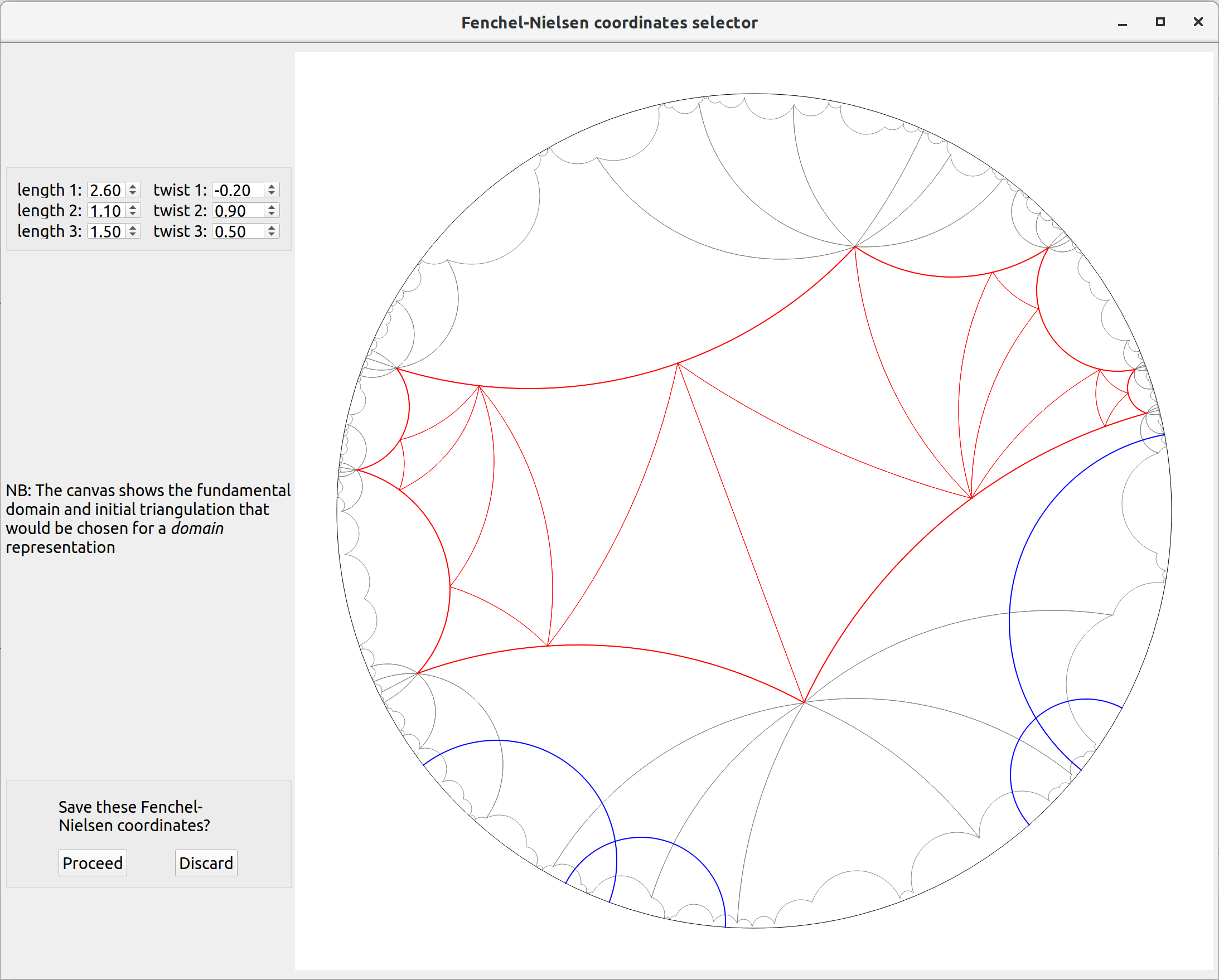
From there you can pick Fenchel-Nielsen coordinates of your choosing for the representation. The canvas shows a fundamental domain for the generated Fuchsian group and a triangulation of it. The blue arcs represent the axes of the generators of the Fuchsian group. As an alternative to the "Fenchel-Nielsen" selector, you can choose a "random" Fuchsian representation, or, in genus 2, the token "nice" Fuchsian representation represented below:


Once both left and right representations are set, the program will compute a triangulation of the domain surface according to the mesh depth, and an initial "piecewise linear" equivariant map from the domain to the target:


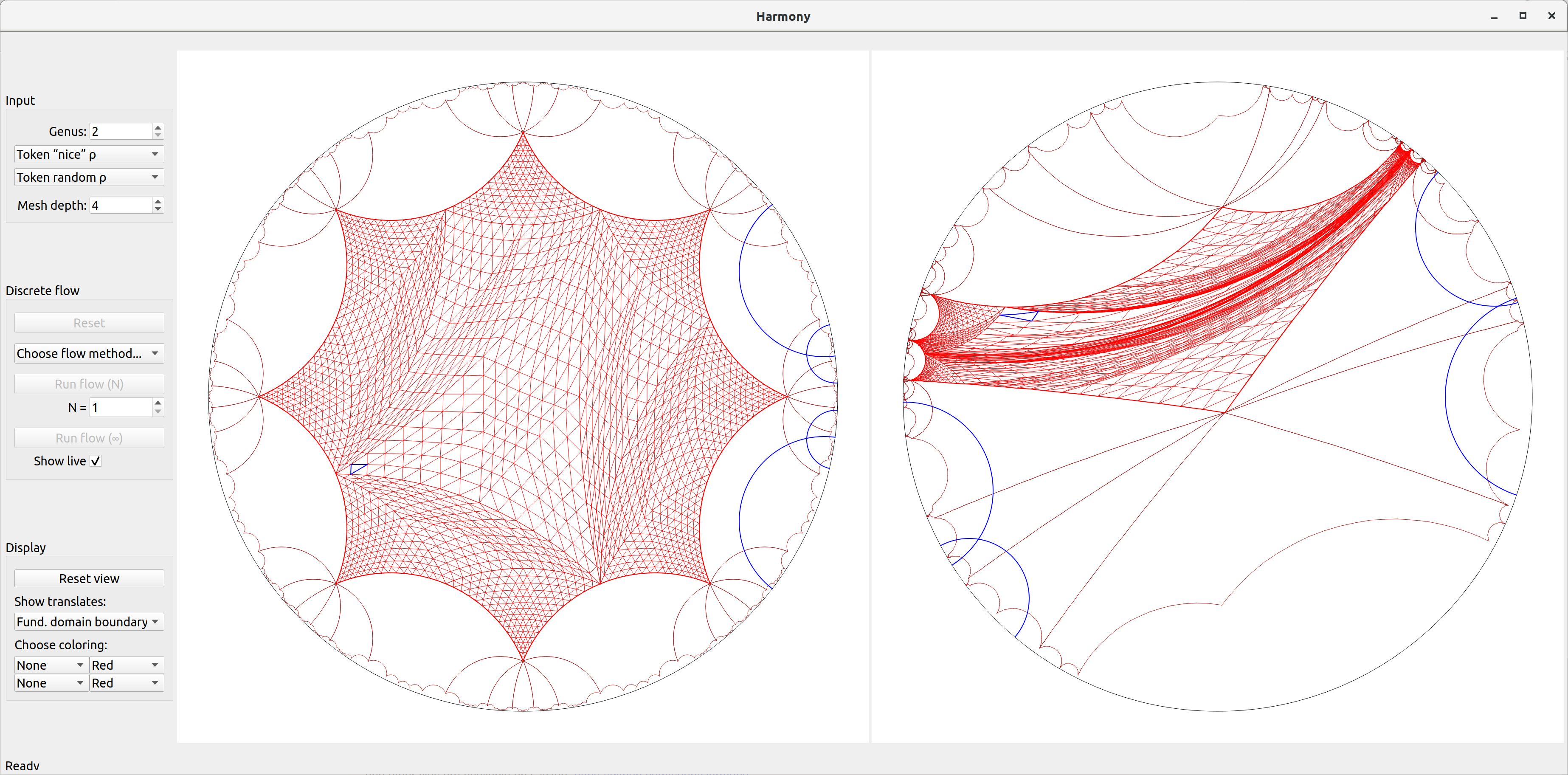
The map is "visualized" by matching each triangle on the left to a triangle on the right. You can hover the mouse over the triangles in order to see matching triangles (highlighted in blue).

You are now ready to run the algorithm for finding the unique discrete equivariant harmonic map. First you need to choose a flow method from the menu: cosh-center of mass method, discrete heat flow (constant step), or discrete heat flow (optimal step). At this stage, the most effective in practice is the cosh-center of mass method. The optimal step discrete heat flow is not a good practical choice: the number of iterations is usually less than the constant step discrete heat flow, but the time of execution is far greater.

You can now hit the "Run flow (∞)" button to run the algorithm. Make sure you keep the box "Show live" checked in order to visualize the flow. The flow will stop when the target precision is reached, or when you hit the "Stop" button.


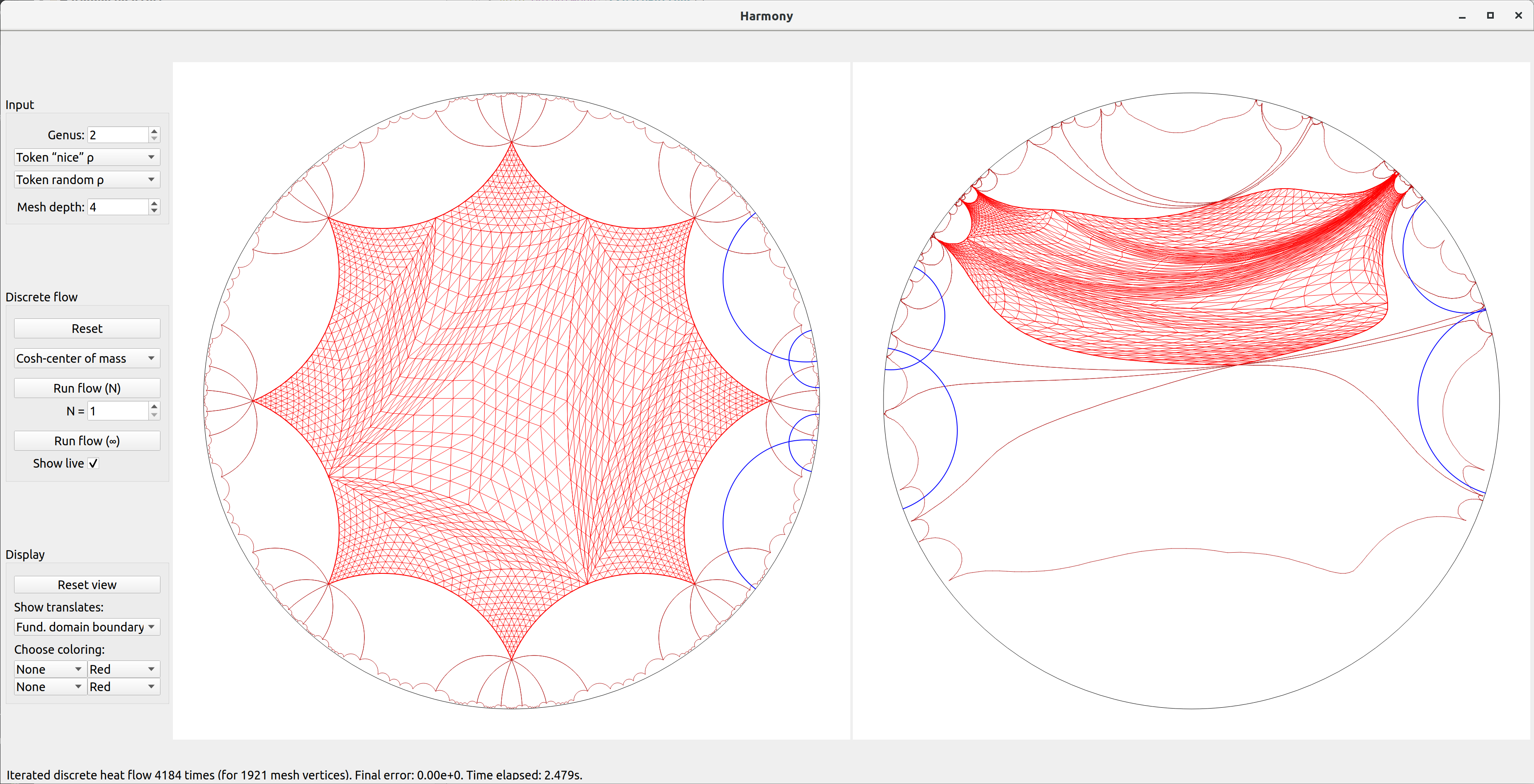
After the harmonic map has been computed, you should explore the display options to visualize it in different ways. The display menu on the left allows you to change the color, to draw translates around a vertex or all vertices (by default, only fundamental domains are shown). You can also change the coloring style from "None" to "Plain": the triangles in the image will then be drawn lighter or darker depending on how contracting or dilating the map is:


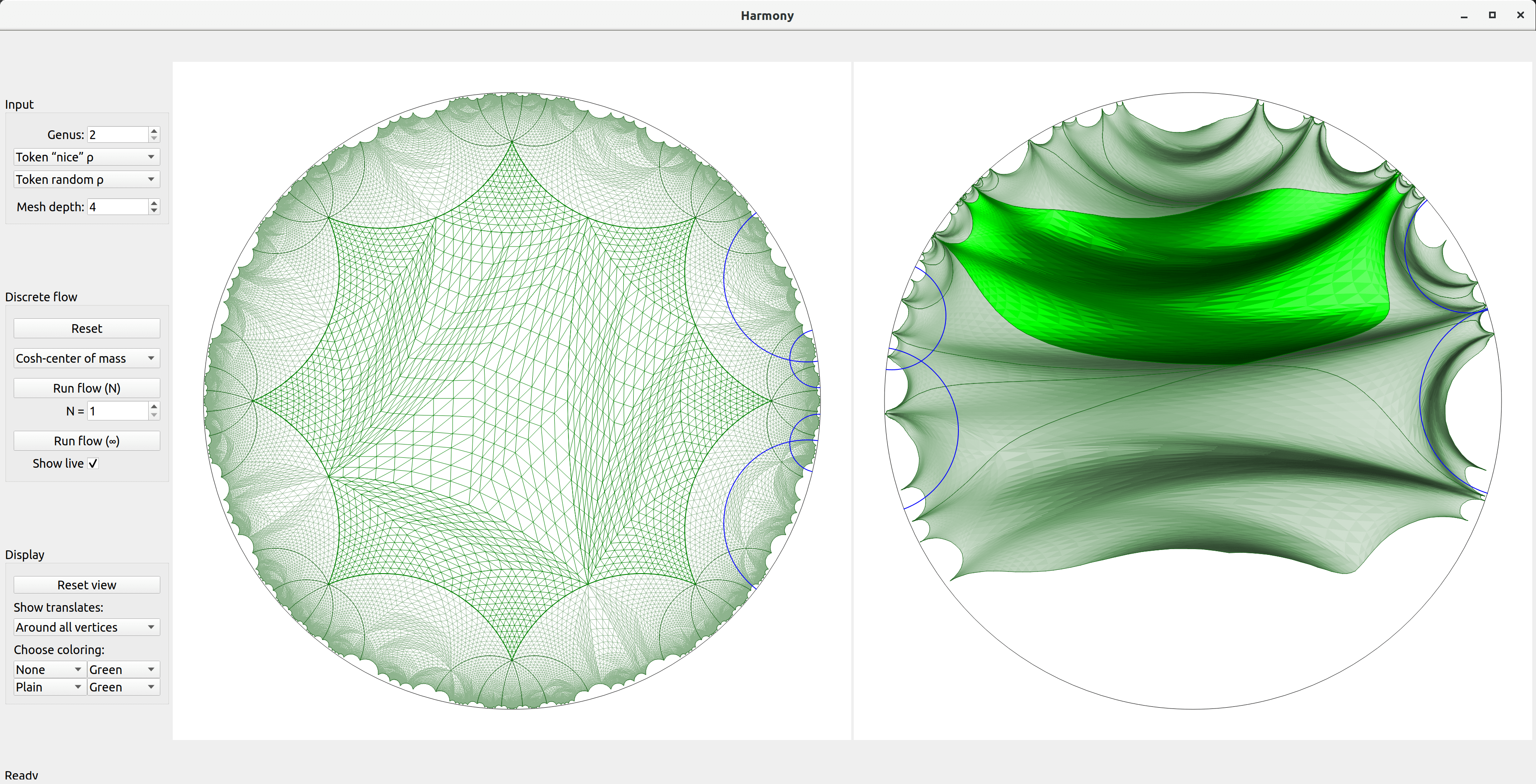
You can also play with the display of either hyperbolic planes with the following controls:


About the program

The program was coded in C++ using the Qt framework. It is free and open source (under the GNU General Public License), all the sources and other files are available on GitHub: https://github.com/seub/Harmony.